Perceptron
- 뉴런을 본따 만든 알고리즘 하나의 단위
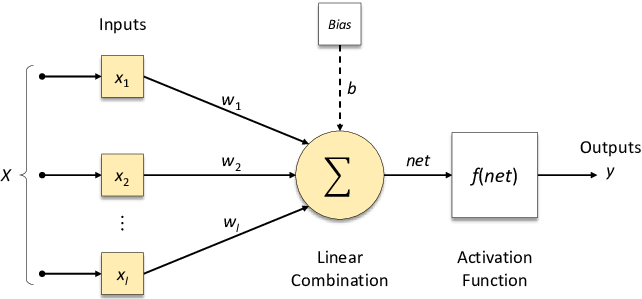
참고: 이미지에서 hidden layer
Input : Visible pixels
1rd hidden layer : edges
2nd hidden layer : corners and contours (simple shapes)
3rd hidden layer : object parts (shapes)
Output : object identity
가장 적합한 θ들의 set 찾기 위한 2가지 연산
1. 넘겨져 온 데이터와 θ들의 Linear Combination 계산 (행렬 합&곱)
- GPU가 행렬 빠르게 연산
2. 선형결합 결과에 Activation Function (활성화 함수) 적용
- Linear Combination의 결과값이 Non-linear Function을 거치게 하여 최종 출력값 계산
- Activation function 거치지 않는다면 아무리 layer를 쌓아도 결국 Linear Regression
- 선형 함수로 표현하지 못하는 것을 비선형 함수로 푸는 것
Activation Functions (활성화 함수), g(x)
[이전 레이어의 모든 입력에 대한 가중 합]을 받아 출력값을 생성하여 다음 레이어로 전달하는 비선형 함수

- 알고가면 좋은 지식1
(Perceptron 하나를 미분한 값) * (현재의 Error) = (한 단계 과거의 Error)
위에서 동그라미 하나가 Perceptron 하나를 의미한다.
각각 최적의 파라미터 θ를 구하기 위해 반복해서 한 단계 전의 layer로 가서 weight를 조정해주어야 한다.
그렇게 하기 위해서는 활성화 함수, g(x)가 미분 가능해야 한다.
- 알고가면 좋은 지식2
인공 신경망 내부에서는 Learnable Kernel을 사용해서 새로운 차원을 만든다.
100행이 있었다고 가정해보자.
Input : (100,3)
kernel1 : (3,4)
1st hidden layer : (100,4)
kernel2 : (4,2)
2nd hidden layer : (100,2)
kernel3 : (2,2)
Output : (100,2)
1. Step 함수

- 0에서 미분 불가능
- Linear Combination 값이 0.00000이 나올 가능성은 없다고 생각해도 Step Function은 어느 x에서나 미분해도 결과값이 0이기 때문에 의미가 없음
- 현재는 아예 쓰지 않음
2. Sigmoid 함수

- 미분 가능
- 하지만, 미분한 값이 너무 작음 (미분한 값이 가장 높은 것이 0.25)
- 5단계만 이전으로 가도 0.25^5=0.001
- 판단의 기준인 Error값이 너무 희미해져서 의미가 없음 = Vanishing Gradient
(레이어가 깊어질수록 앞선 오차 값이 역방향으로 뒤까지 전달되지 않는 문제 발생)
- 현재는 거의 쓰지 않음
3. tanh

- sigmoid 함수에서 y값의 범위를 0~1로 늘려줌
- 텍스트 분석에서는 tanh의 성능이 좋을 때도 있음
4. ReLU
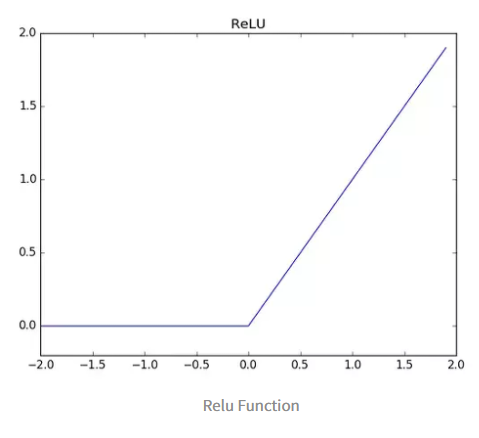
- 미분했을 때 값이 0 또는 1
- 성능이 좋음 (대부분 사용 추천)
5. LeakyReLU

활성화 함수 정리

활성화 함수 활용
- 결과값을 그대로 받아 Regression
- Sigmoid를 거쳐 Binary Classification (하나의 ouput 받아서 sigmoid / 두 output 받아서 softmax)
- Softmax를 거쳐 k-class Classification
'멋쟁이 사자처럼 AI SCHOOL 5기 > Today I Learned' 카테고리의 다른 글
| [7주차 총정리] Neural Network에서 오버피팅 피하는 방법 (Dropout, Batch normalization) (0) | 2022.04.28 |
|---|---|
| [7주차 총정리] Gradient Descent 활용한 신경망 학습 과정 (Neural Network Optimization) (0) | 2022.04.28 |
| [7주차 총정리] 정형데이터를 위한 인공신경망 모델, TabNet 기초 정리 (0) | 2022.04.27 |
| [7주차 총정리] Deep Learning 기초 개념 정리 (0) | 2022.04.26 |
| [7주차 총정리] Transfer Learning(전이학습) 개념 정리 (0) | 2022.04.26 |
